Solución RETO 3

Hola a todos, pasamos a solucionar el reto de la semana pasada de tres formas diferentes, una de ellas asequible para cualquiera con un poco de visión espacial, y otra forma mediante cálculo matemático. La tercera nos la envía como solución nuestra compañera Carmen Borrás y la añadimos también como variante de la primera.

SOLUCIÓN 1

Antes de "perdernos" en cálculos pitagóricos y operaciones podemos caer en la cuenta de que jugando con las superficies que tenemos (que suman 1 metro cuadrado) podemos obtener 5 cuadrados como el que nos piden calcular la superficie, por tanto 1 metro cuadrado entre 5 es 0,2 metros cuadrados.

SOLUCIÓN 2
 En esta resolución partimos de unas consideraciones...

Por tanto H = a+b+c
Si averiguamos H, a y c podríamos calcular b, y elevando b al cuadrado tendríamos el área pedida.

AVERIGUAMOS H:
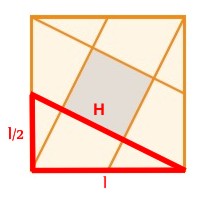
Por una parte tomamos el siguiente triángulo rectángulo y aplicamos el teorema de Pitágoras...

Sabemos que el lado es 1 pero lo dejamos indicado en el proceso. De la figura tenemos que...

AVERIGUAMOS a y c:

Tomamos ahora el siguiente triángulo rectángulo observando la siguiente relación: c = 2·a

Aplicamos el teorema de Pitágoras realizando los siguientes cálculos...

CÁLCULO FINAL

Conociendo H, a y c podemos despejar b de la fórmula...

H = a+b+c   ...de manera que... b = H-a-c

Obtenemos así el mismo resultado que en la primera solución.

SOLUCIÓN 3

Esta solución nos la remite Carmen Borrás:
El cuadrado grande (1 m2) puede dividirse en 20 triángulos rectángulos iguales, con una superficie de 0,05 m2, como puede apreciarse en la figura. El cuadrado central está formado por cuatro triángulos por tanto su superficie es de 0,2 m2.

Y LOS GANADORES DE ESTA SEMANA SON...

SECCIÓN ADULTOS: CARMEN BORRÁS, RUBÉN ESPINOSA, ANA NATEK.

SECCIÓN ALUMNOS: ÁNGEL FERRER, VICENT GOMIS.